使用函数法计算设备组合加工工时

这样的工时有以下不足：

1. 因为数据是分段式的，所以比较粗糙；

2. 数据相关之间没有逻辑关系和联系；

3. 一旦其中的加工要求未考量在其中，那么其对应的标准数据就可能无法适合，还得重新再定义； 

此文的原理适合：

1. 以切线动作为基础和范例，并包括同步衍生出其他工艺的综合性大工位工艺。

2. 可以推广到所有包括裁切或者纯机械自动化加工的工序；

比如我们常说的裁切，其实在设备能力范围内与在自身需求下，衍生出来的动作和功能模块也是很多的。以下的层级就是随着自动化功能的增加而逐渐增加；

1. 常见的线缆裁切机上有基本的开线口和半剥/全剥两个功能。

2. 在这上面可以增加新的不同模块，如捻线，上锡，多线同时作业，折线等一系列功能。

3. 再和打端子的工艺再串联起来，就变成了连切带打端子的机器了，在这上面就又可以扩展出新的功能模块：打端子，穿防水塞，切/套热缩管，收缩热缩管等。

4. 也可以扩展到自动组装连接器等工艺上，那么自动化程度就越来越高了：入端子，入盲堵等。

5. 当然市面上也有从前工序到最后的成品一直最后包装的一条龙的自动化设备或者产线。不过因为线束产品本身就是非标性，当其数量与利润无法支撑这个投资的时候，就没有可投资的价值。所以市面上也只有针对少量的简单的线束产品的自动化设备实现出来了。

但是就其市场与技术而言，可以这么说，只要有需要，就能找到，也能做出任何一种（半）自动化等级的设备来对应满足。对于这样的最终工时，很多 IE 就是依靠测量手法，再加上 OE 和 IE 的技能进行综合处理而来。而此处抛开那些专业的技能和手法，仅仅以纯数学的理论来讨论如何确定设备作业工时，并提供大家一个新的解决思路：

我将其定义为函数法；也就是将其中所有的动作进行细化定义为一个标准模块，然后，根据后续设备加工工艺要求不同，就可以自行组合成新的任意变量下的工时；其公式定义为：

T=K(A*a+B*b+C*c+D*d……Z*z)/µ--------- 公式 1

T：工时；单位秒；

K：IE/OE 的技能系数或者为调整系数，根据实际生产需求（如现场管理所产生的模具更换，机器维护，维修保养，异常停机等综合性的平均损耗），因为在此处不予考虑，因此系数暂定为 1；

A,B,C,D……Z：某个工序动作的标准时间，理论上可以是无限个连贯性的动作；

a,b,c,d……z：对应该工序动作的作用倍数系数，以设备动作加工的次数而定。取值范围为正整数和0。如果没有这个动作，那么系数就是为 0。一般线缆作业的两端上进行加工，因此大部分动作的系数为1或者2；当然也有特殊的情况，如中剥工艺。在常用的电脑裁切机中，理论上的中剥点最大可以达到 7 次，而且每个中剥点都是依次完成的，并非并行同步完成，所以此时如果有此工艺要求，那么的中剥系数就变成了 7；

µ：整体同时加工的倍数关系系数；比如目前某些设备一次可以连切带剥 5 根线，而不再是传统的 1 根线了，那么此时的系数就变成了 5。但是也发现，该系数只会影响到最终的工时 T，是与设备的功能模块工时没有关系的，只对于 IE 定义最后单根产品的工时有关系，所以此处也不是重点要研究的内容。

综合总结，该公式的适合范围如下：

1. 纯机械设备的加工，非人工作业生产；

2. 可以为单机或者流水线式生产，而且每个工序式连贯的，相互工序之间最好不能不能有非必要的等待时间，至少不能有不规则的等待时间或者对实际作业影响很大的非必要等待时间，而影响其精度；

3. 机器设备上的参数与设置必须要固定（具体原因后续会说明）；我们以最常见的电脑裁切机（如图 1）作为示范：

图 1：电脑裁切机

我们经常会拿着这样的机器所做的工艺就是切线，切线+开单端外皮，切线+双端外皮三种加工。明显的最后的这套动作是包含前面的，所以以这套常规动作进行举例分析：经过个人观察和理解，其机器的整个作业过程与方法如下：

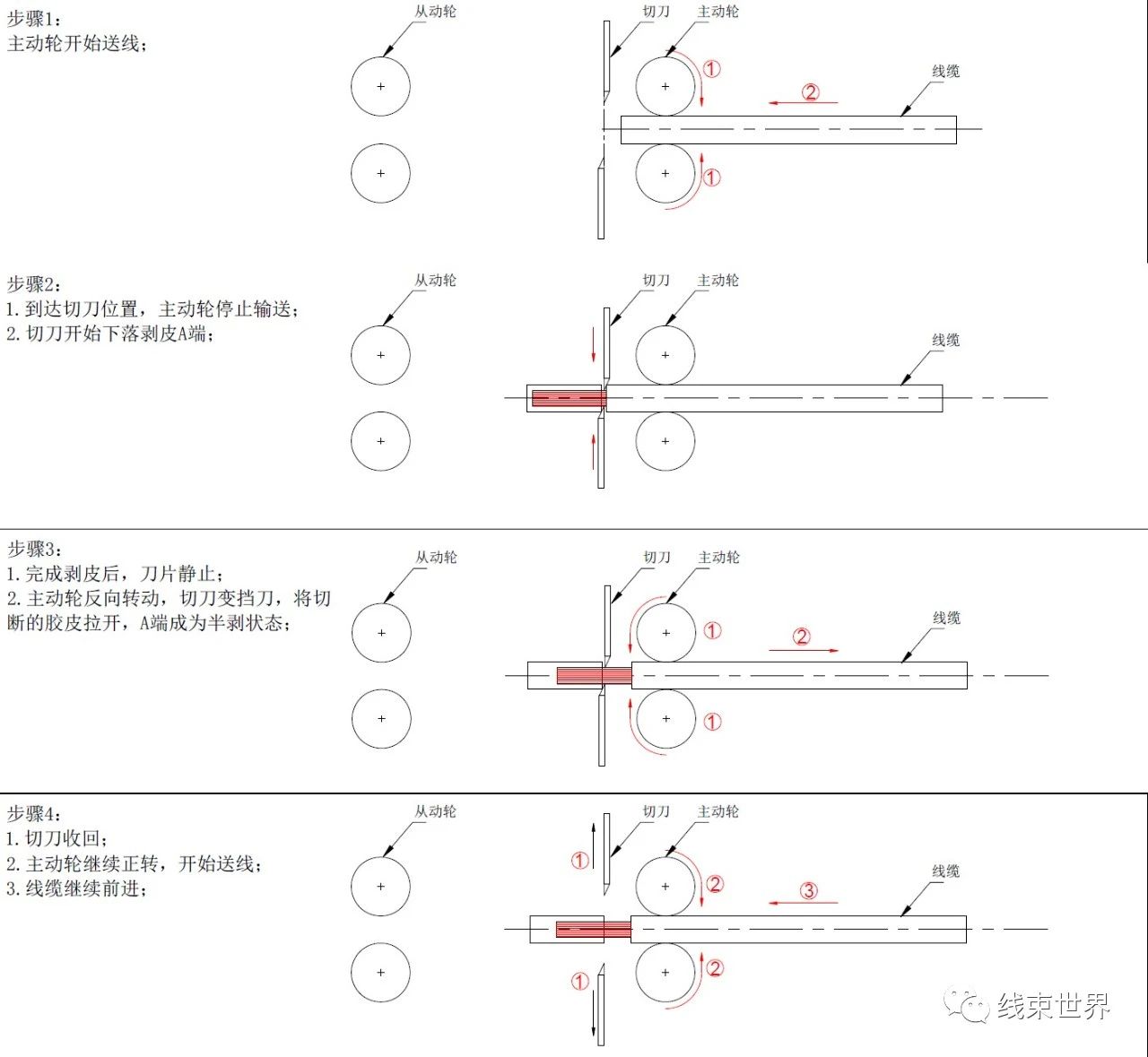
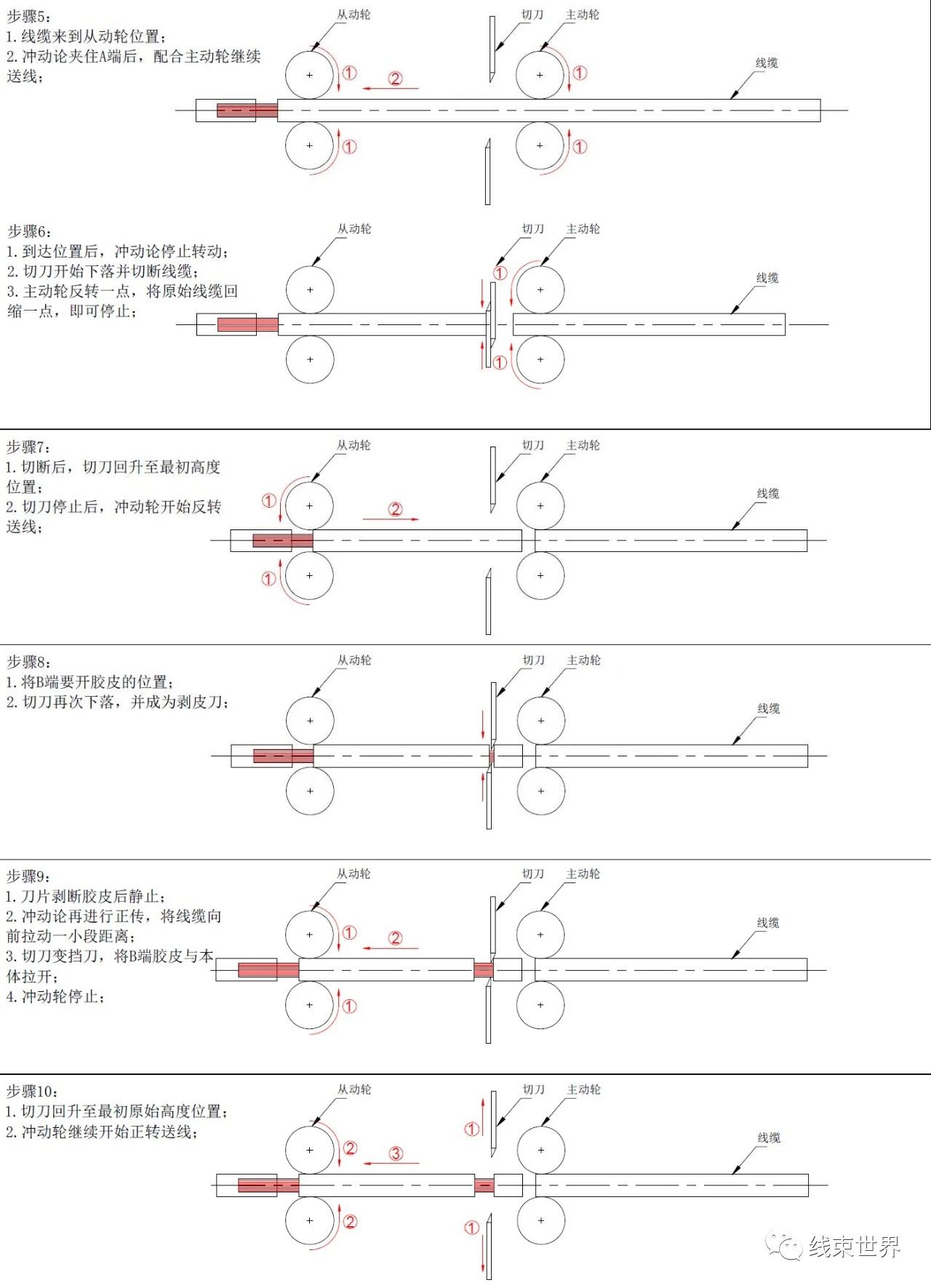
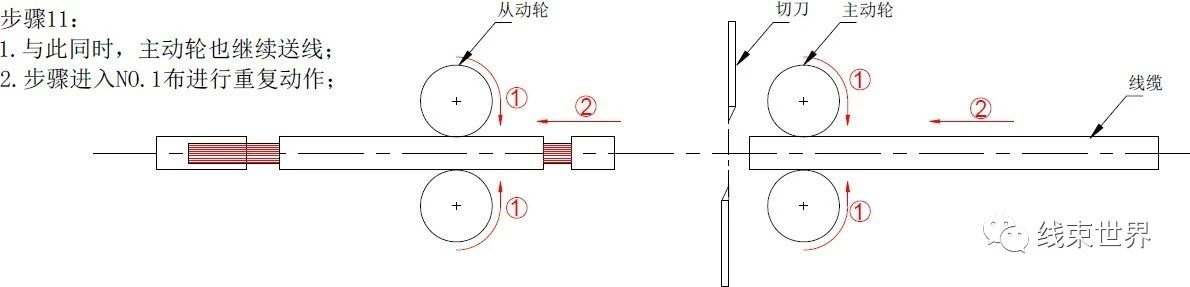
图 2：裁线+（中）剥皮过程

通过以上示意图，可以发现：

1. 机器主要作用工作部件就是滚轮和切刀；

2. 按照工序来模块划分，而机器的主要的几个动作模块就是送线，切线，剥线，半剥；

3. 再分析以上 4 个动作模块，与设备主要工作部位的对应关系就是

3.1 送线和半剥：对应滚轮；

3.2 切线和剥线：对应切刀；

4. 所以将以上 4 个动作模块与公式 1 进行结合：

4.1 分别确定其对应的标准时间为 A,B,C,D：在设备参数固定的前提下，送线动作的时间和线长有着正比的关系：比如送线速度为 1.0m/S，那么如果我的线长为 1m，那么送线时间就是 1S，当线长变为 2 时，那么送线时间就是 2S；

4.2 其对应的 a,b,c,d 数据就是 1，2，2，2；

4.3 µ：一次切一根，所以该参数也取值为 1；

4.4 K：这个和每个公司与人员的标准不同而取值不同，此处不做研究，暂定为 1；

5. 设定完公式中参数后，按照以下情况对总工时的进行取值：

5.1 所以可以初步定义线长为 1m;如果考虑到材料的浪费与损耗，也可以自定义为 0.1m 等均可；但是在最后的公式 5 中要转换为单位长度上的送线时间；

5.2 使用只有切线的功能时，连续量测 50PCS 的整个时间T0；

5.3 再调整线长(比如这次定义为 2m)，同样再次量测 50PCS 的整个时间 T1；

5.4 这样就能得到一个引申出来的公式组（见公式 2~4）：

T0=A0+2B---------------- 公式 2

T1=A1+2B---------------- 公式 3

如 4.1 所阐述，送线时间与线长是正比关系。所以 A0 与 A1 的关系有个系数υ的关系，而这个系数就是前后两次切线长度（L0 和 L1）的比值，即：

Υ=L1/L0=A1/A0----- 公式 4；

通过以上公式组就可以知悉，T0,T1 以及 A1 与 A2 的关系，就变成了一个最简单的二元一次方程了。就能求出 A0,A1 以及B 值了；

6. 同理，可以按照此方法，再依次增加上C 的动作与时间，再测试出 T2 的数据，求出 C 的工时；

7. 以此类推，就可以得到A,B,C,D 的单工作标准工时了；

8. 此时公式 1 就变化为公式 5：

T=LA+2B+C*c+D*d---------------- 公式 5

切记：此时的 A 是单位长度(如 1 米)的送线时间；

此时公式 5 中的 A,B,C,D 就变成了常数。就对于新的需求时，只需要只需要确认新需求的参数即可：切线长度多少；切点一定是两头都要切的，所以 b=2；要剥线或半剥 1 端还是两端？（切记：剥线和半剥是对立的，不是并存的）。这样就能得到所需要的设备模块动作的纯加工时间以及关系式。这样出来的公式就能对于任何一个细节和细微差别的加工条件，就都能立刻取得其工时；

注意事项：

1. 因为设备加工速度很快，且是连续性加工作业；因此为了提高精度，就需要进行连续采样；在连续生产的前提下，数量越大，单套工作也越精准；

2. 对几个工序进行排列组合并进行取舍，从而造成单套工作时间上的差异；当然，其中的参数变化越大，则出现的差异也越大，越对后面的计算有帮助；

3. 因为要考虑和计算到设备各个模块的工作时间，因此，在调整单元模块的时候，整个所有的计算公式中均要将这些模块工时包含在其中。这样才能求出A,B,C,D 的数值；

4. 务必知悉：该公式是建立在机器设备的正常运作前提下，因此，务必要确保在取参时的设备工作的参数的固定和稳定，如转轮的速度，气压大小等等。特别时裁切机上的转轮速度时可调的，而其速度就直接关系到了送线的速度了。所以即使相对一样的线长时，转速不同，那么对应的送线时间也就不同了。所以这些参数和设备都必须要固定；

5. 同理，因为是后续为定工时做准备的，因此，这些设备的参数定义也务必要和量产时的设备调参一致，否则，出来的数据不能直接借鉴和使用，还需要进行再次调整和转化；

1.  最初定义切线长度为 1m，只有切线功能，连续测量 50PCS 的总时间为 71.6 秒。所以，71.6=（A+2B）*50；

2.  将切线长度改为 2m，一样也只采用切线的功能，连续测量的总时间为 110.5 秒。所以 110.5=（2A+2B）*50;

3. 所以可以求出：A=0.778，B=0.327；

4.  因此基础的公式就变为了 T=0.778L+2*0.327；输入任何一个长度 L，都可以知道加工时间了；

5.  同理，按照 NO.1~NO.4 的方法再增加其他工艺，如剥线，上锡等；将公式范围放宽并涵盖其设备的加工内容即可；

当然为了识别和记忆方便，这些模块的加工系数的精度后续也可以根据自己的喜好进行取舍。这样就能针对某个自动化设备定出其加工公式了。后续对新产品的加工时间评估，将此公式一套用，都可以立马得出一个精准的数据来；举一反三，这样的办法对于如切管，连切带打等设备的那样工序，也同样适用；